गणित में विभाजन (Division) एक ऐसी प्रक्रिया है जो संख्याओं को छोटे-छोटे हिस्सों में बाँटने में मदद करती है। इस प्रक्रिया में चार मुख्य शब्दावलियाँ सामने आती हैं: भाज्य (Dividend), भाजक (Divisor), भागफल (Quotient), और शेषफल (Remainder)। ये शब्द न केवल स्कूली गणित में बल्कि प्रतियोगी परीक्षाओं और रोज़मर्रा के जीवन में भी महत्वपूर्ण हैं। इस लेख में हम इन अवधारणाओं को सरल हिंदी में समझाएँगे और उनके उपयोग को उदाहरणों के साथ स्पष्ट करेंगे।
भाज्य, भाजक, भागफल और शेषफल क्या हैं?
1. भाज्य (Dividend)
भाज्य वह संख्या है जिसे हम विभाजित करते हैं। यह वह मूल संख्या है जिसे छोटे हिस्सों में बाँटा जाता है।
- उदाहरण: यदि 15 को 3 से विभाजित करते हैं, तो 15 यहाँ भाज्य है।
2. भाजक (Divisor) (H3)
भाजक वह संख्या है जिसके द्वारा हम भाज्य को विभाजित करते हैं। यह निर्धारित करता है कि भाज्य को कितने हिस्सों में बाँटा जाएगा।
- उदाहरण: उपरोक्त उदाहरण में, 3 भाजक है।
3. भागफल (Quotient)
भागफल वह परिणाम है जो हमें तब मिलता है जब भाज्य को भाजक से पूर्ण रूप से विभाजित कर लिया जाता है। यह बताता है कि भाजक कितनी बार भाज्य में समा सकता है।
- उदाहरण: 15 ÷ 3 = 5, यहाँ 5 भागफल है।
4. शेषफल (Remainder)
शेषफल वह संख्या है जो विभाजन के बाद बच जाती है, जब भाज्य को भाजक से पूर्ण रूप से विभाजित नहीं किया जा सकता।
- उदाहरण: यदि 17 को 5 से विभाजित करें, तो 5 में 17 तीन बार (3 × 5 = 15) समा सकता है और 2 बचता है। यहाँ 2 शेषफल है।
विभाजन का मूल सूत्र
विभाजन की प्रक्रिया को समझने के लिए एक महत्वपूर्ण सूत्र है:
भाज्य = (भाजक × भागफल) + शेषफल
सूत्र का उपयोग कैसे करें?
- यह सूत्र हमें चारों अवधारणाओं के बीच संबंध को समझने में मदद करता है।
- उदाहरण: 1253 में 3 का भाग करने पर
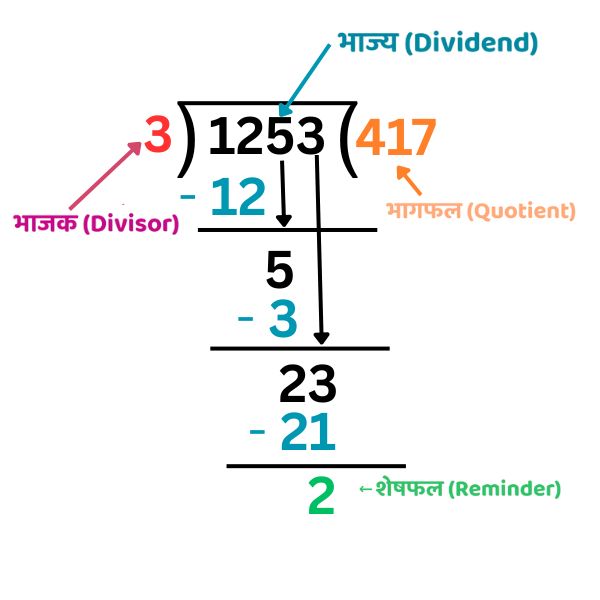
शेषफल की विशेषताएँ
शेषफल कुछ विशेष गुणों के साथ आता है जो गणितीय गणनाओं में उपयोगी होते हैं:
- न्यूनतम मान: शेषफल का न्यूनतम मान हमेशा 0 होता है (जब भाज्य पूर्ण रूप से विभाज्य हो)।
- अधिकतम मान: शेषफल का अधिकतम मान भाजक से एक कम होता है।
- उदाहरण: यदि भाजक 5 है, तो शेषफल 0, 1, 2, 3, या 4 हो सकता है।
विभाजन के नियम और उपयोग
विभाज्यता के नियम
विभाज्यता के नियम यह निर्धारित करते हैं कि कोई संख्या किसी दूसरी संख्या से पूर्ण रूप से विभाजित हो सकती है या नहीं। कुछ सामान्य नियम:
- 2 से विभाज्यता: संख्या का अंतिम अंक 0, 2, 4, 6, या 8 हो।
- 3 से विभाज्यता: संख्या के अंकों का योग 3 से विभाज्य हो।
- 5 से विभाज्यता: संख्या 0 या 5 पर समाप्त हो।
रोज़मर्रा के जीवन में उपयोग
- वित्तीय हिसाब: बिल बाँटते समय या ब्याज की गणना में।
- समय प्रबंधन: कार्यों को समान समय में विभाजित करना।
- प्रतियोगी परीक्षाएँ: SSC, UPSC, और बैंकिंग परीक्षाओं में विभाजन से संबंधित प्रश्न आम हैं।
उदाहरणों के साथ अभ्यास
आइए कुछ उदाहरणों के साथ इन अवधारणाओं को और स्पष्ट करें:
उदाहरण 1:
प्रश्न: 48 को 7 से विभाजित करने पर भागफल और शेषफल क्या होगा?
हल:
- 7 में 48 को 6 बार (6 × 7 = 42) समा सकता है।
- शेष = 48 – 42 = 6
- उत्तर: भागफल = 6, शेषफल = 6
उदाहरण 2:
प्रश्न: यदि भाजक = 9, भागफल = 12, और शेषफल = 5 है, तो भाज्य क्या होगा?
हल:
- सूत्र: भाज्य = (भाजक × भागफल) + शेषफल
- भाज्य = (9 × 12) + 5 = 108 + 5 = 113
- उत्तर: भाज्य = 113
सामान्य गलतियाँ और उनसे बचने के तरीके
- गलती 1: शेषफल को नकारात्मक मान लेना।
- समाधान: शेषफल हमेशा 0 या धनात्मक होता है।
- गलती 2: सूत्र में गलत मान डालना।
- समाधान: हमेशा सुनिश्चित करें कि आप सही संख्या को सही स्थान पर रख रहे हैं।
- गलती 3: विभाज्यता नियमों को भूल जाना।
- समाधान: नियमों को बार-बार दोहराएँ और अभ्यास करें।
निष्कर्ष
भाजक भाज्य भागफल शेषफल गणित की आधारभूत अवधारणाएँ हैं जो हर स्तर पर उपयोगी हैं। इनके सूत्र और नियमों को समझकर आप न केवल स्कूली गणित में बल्कि प्रतियोगी परीक्षाओं और रोज़मर्रा की गणनाओं में भी सफल हो सकते हैं। नियमित अभ्यास और उदाहरणों को हल करने से आप इन अवधारणाओं में निपुणता हासिल कर सकते हैं।
क्या आप गणित को और आसान बनाना चाहते हैं? नीचे कमेंट करें और हमें बताएँ कि आप किस टॉपिक पर और जानना चाहते हैं!
